PhaseIdealLoop::Dominators() 函数的探究

这里描述了 OpenJDK8 中构建 Dominator Tree 的理论依据和编码实践。

Lengauer & Tarjan \(O(m\alpha(m, n))\) algorithm 概述

• Let \(G = (V, E, r)\) be a flowgraph with start vertex \(r\). A vertex \(v\) dominates another vertex \(w \ne v\) in \(G\) if every path from \(r\) to \(w\) contains \(v\). Vertex \(v\) is the immediate dominator of \(w\), denoted \(v = idom(w)\), if \(v\) dominates \(w\) and every other dominator of \(w\) dominates \(v\).

• THEOREM 1. Every vertex of a flowgraph \(G = (V, E, r)\) except \(r\) has a unique immediate dominator. The edges \(\{(idom(w), w) \mid w \in V - \{r\}\}\) form a directed tree rooted at \(r\), called the dominator tree of \(G\), such that \(v\) dominates \(w\) if and only if \(v\) is a proper ancestor of \(w\) in the dominator tree. See Figures 1 and 2.¹,²

  Fig.1. A flowgraph

  graph TD; R((R)) --> A((A)); R --> B((B)); R --> C((C)); A --> D((D)); B --> A; B --> D; B --> E((E)); C --> F((F)); C --> G((G)); D --> L((L)); E --> H((H)); F --> I((I)); G --> I; G --> J((J)); H --> E; H --> K((K)); I --> K; J --> I; K --> R; K --> I; L --> H;

  Fig.2. Dominator tree of flowgraph in Fig.1

  graph TD; R((R)) --> I((I)); R --> K((K)); R --> C((C)); C --> F((F)); C --> G((G)); G --> J((J)); R --> H((H)); R --> E((E)); R --> A((A)); R --> D((D)); D --> L((L)); R --> B((B));

• Every vertex is an ancestor and a descendant of itself.³

• LEMMA 1. If \(v\) and \(w\) are vertices of \(G\) such that \(v \leqslant w\), then any path from \(v\) to \(w\) must contain a common ancestor of \(v\) and \(w\) in \(T\).

  Proof. 由于 \(v \leqslant w\)，所以 \(v\) 只可能来自于 \(w\) 的祖先节点或者是 preorder 小于 \(w\) 的兄弟节点，如果来自祖先节点则 \(v\) 和 \(w\) 的公共祖先节点显然应该是 \(v\)，否则，从 \(v\) 到 \(w\) 的路径必然需要经过 \(w\) 的祖先节点，因为如果不经过 \(w\) 的祖先节点，在做 DFS 时就应该将 \(v\) 和 \(w\) 放入同一棵子树中，而这与 \(v\) 来自兄弟节点的假设矛盾，所以路径中必定存在 \(v\) 和 \(w\) 共同的祖先节点。更加详细的证明请参考 ⁴ \(\Box\)

• LEMMA 2. For any vertex \(w \ne r\), \(idom(w) \xrightarrow{+} w\)⁵.

  Proof. \(w\) 的任何一个 dominator 肯定在 \(r\) 到 \(w\) 的任意一个路径上，从而也肯定在 \(T\) 的任意 \(r\) 到 \(w\) 的路径上 \(\Box\)

• \(sdom(w) = min\{v \mid\) there is a path \(v = v_0, v_1, \ldots, v_k = w\) such that \(v_i > w\) for \(1 \leqslant i \leqslant k - 1\}\). (1)

• LEMMA 3. For any vertex \(w \ne r\), \(sdom(w) \xrightarrow{+} w\).

  Proof.1. 这里从 \(sdom(w)\) 的定义可以得到：如果 \(w\) 的前继节点来自 \(w\) 的祖先节点，则 \(sdom(w)\) 为该前继节点；如果前继节点来自 \(w\) 的 preorder 大于 \(w\) 的兄弟节点，根据 \(sdom(w)\) 的定义，\(sdom(w)\) 肯定为 \(w\) 的某一祖先节点；如果前继节点来自 \(w\) 的子孙节点，则递归使用这个过程分析。所以无论如何，\(sdom(w)\) 肯定是 \(w\) 的某一祖先节点，且至少是其父节点 \(\Box\)

  Proof.2『更加形式化的证明』. Let \(parent(w)\) be the parent of \(w\) in \(T\). Since \((parent(w), w)\) is an edge of \(G\), by (1) \(sdom(w) \leqslant parent(w) < w\). Also by (1), there is a path \(sdom(w) = v_0, v_l, \ldots, v_k = w\) such that \(v_i > w\) for \(1 \leqslant i \leqslant k - 1\). By Lemma 1, some vertex \(v_i\) on the path is a common ancestor of \(sdom(w)\) and \(w\). But such a common ancestor \(v_i\) must satisfy \(v_i \leqslant sdom(w)\). This means \(i = 0\), i.e. \(v_i = sdom(w)\), and \(sdom(w)\) is a proper ancestor of \(w\). \(\Box\)

• LEMMA 4. For any vertex \(w \ne r\), \(idom(w) \xrightarrow{*} sdom(w)\).

  Proof. By Lemmas 2 and 3, \(idom(w)\) and \(sdom(w)\) are proper ancestors of \(w\). The path consisting of the tree path from \(r\) to \(sdom(w)\) followed by a path \(sdom(w) = v_0, v_1, \ldots, v_k = w\) such that \(v_i > w\) for \(1 \leqslant i \leqslant k - 1\) (which must exist by (1)) avoids all proper descendants of \(sdom(w)\) which are also proper ancestors of \(w\). It follows that \(idom(w)\) is an ancestor of \(sdom(w)\). \(\Box\)

• LEMMA 5. Let vertices \(v\), \(w\) satisfy \(v \xrightarrow{*} w\). Then \(v \xrightarrow{*} idom(w)\) or \(idom(w) \xrightarrow{*} idom(v)\).

  Proof. Let \(x\) be any proper descendant of \(idom(v)\) which is also a proper ancestor of \(v\). By Theorem 1 and Corollary 1, there is a path from \(r\) to \(v\) which avoids \(x\). By concatenating this path with the tree path from \(v\) to \(w\), we obtain a path from \(r\) to \(w\) which avoids \(x\). Thus \(idom(w)\) must be either a descendant of \(v\) or an ancestor of \(idom(v)\). \(\Box\)

• THEOREM 2. Let \(w \ne r\). Suppose every \(u\) for which \(sdom(w) \xrightarrow{+} u \xrightarrow{*} w\) satisfies \(sdom(u) \geqslant sdom(w)\). Then \(idom(w) = sdom(w)\).

  Proof. 对于任何一条从 \(r\) 到 \(w\) 的路径 \(p\)，设 \(x\) 是 \(p\) 上最后一个满足 \(x < sdom(w)\) 的节点。如果不存在这样的节点，则 \(sdom(w)\) 就是 \(r\)，因为没有比 \(r\) 更小的节点，而 \(r\) 肯定是 \(w\) 的 dominator。否则，设 \(y\) 是 \(p\) 上 \(x\) 之后最早满足 \(sdom(w) \xrightarrow{*} y \xrightarrow{*} w\) 的节点，设 \(q = (x = v_0, v_l, v_2, \ldots, v_k = y)\) 是 \(p\) 中从 \(x\) 到 \(y\) 的一段子路径，对于其中的 \(v_i\)，\(i\) 满足 \(1 \leqslant i \leqslant k - 1\)，\(v_i > y\)，这个结论可以通过以下证明获得：假设存在某个 \(v_i < y\)，根据 LEMMA 1，存在某个 \(v_j\) 作为 \(y\) 的祖先节点，其中 \(j\) 满足 \(i \leqslant j \leqslant k -1\)，又根据 \(x\) 的定义，\(v_j \geqslant sdom(w)\)，从而得出 \(sdom(w) \xrightarrow{*} v_j \xrightarrow{*} y \xrightarrow{*} w\)，但这个结论和 \(y\) 的定义矛盾。根据 \(sdom\) 的定义可知 \(sdom(y) \leqslant x\)，又因为 \(x < sdom(w)\)，所以 \(sdom(y) < sdom(w)\)。根据 THEOREM 2 的假设，此时 \(y\) 只可能等于 \(sdom(w)\)，从而得到 \(sdom(w)\) 在 \(p\) 中，由于 \(p\) 是任意一条路径，所以 \(sdom(w)\) 是 \(w\) 的 dominator。由于 Lemma 4，所以 \(idom(w) = sdom(w)\)。 \(\Box\)

• THEOREM 3. Let \(w \ne r\) and let \(u\) be a vertex for which \(sdom(u)\) is minimum among vertices \(u\) satisfying \(sdom(w) \xrightarrow{+} u \xrightarrow{*} w\). Then \(sdom(u) \leqslant sdom(w)\) and \(idom(u) = idom(w)\).

  PROOF. 设 z 是一个满足 \(sdom(w) \rightarrow z \xrightarrow{*} w\) 的节点，由于 \(sdom(u)\) 是最小节点，所以 \(sdom(u) \leqslant sdom(z)\)，同时根据 \(sdom\) 的定义，\(sdom(z) \leqslant sdom(w)\)，所以 \(sdom(u) \leqslant sdom(w)\)。

  根据 LEMMA 4，\(idom(w) \xrightarrow{*} sdom(w)\)，而 \(sdom(w) \xrightarrow{+} u\)，所以 \(idom(w) \xrightarrow{+} u\)。根据 LEMMA 5，因为 \(u \xrightarrow{*} w\)，所以要么 \(u \xrightarrow{*} idom(w)\)，要么 \(idom(w) \xrightarrow{*} idom(u)\)，前者明显已经不符合，所以只能是 \(idom(w) \xrightarrow{*} idom(u)\)，如果同时又满足 \(idom(u)\) 是 \(w\) 的某个 dominator，则证明 \(idom(u) = idom(w)\)。

  设任意一条从 \(r\) 到 \(w\) 的路径 \(p\)，设 \(x\) 为 \(p\) 中满足 \(x < idom(u)\) 的最后一个节点，如果不存在这样的 \(x\)，则 \(idom(u) = r\)，从而得到 \(idom(u)\) 是 \(w\) 的 dominator。否则，设 \(y\) 是 \(p\) 中位于 \(x\) 后第一个满足 \(idom(u) \xrightarrow{*} y \xrightarrow{*} w\) 的节点，使 \(q = (x = v_0, v_1, v_2, \ldots, v_k = y)\) 是 \(p\) 中从 \(x\) 到 \(y\) 的一段子路径，如同 THEOREM 2 中的证明，对于 \(q\) 中的 \(v_i\)，其中 \(1 \leqslant i \leqslant k - 1，v_i > y\)，根据 sdom 的定义，\(sdom(y) \leqslant x\)。根据 LEMMA 4，\(idom(u) \leqslant sdom(u)\)。综上，\(sdom(y) \leqslant x < idom(u) \leqslant sdom(u)\)。

  因为 \(u\) 是从 \(z\) 到 \(w\) 的树路径上做 sdom 计算最小的节点，而 \(y\) 也在从 \(r\) 到 \(w\) 的树路径上，根据前面 \(sdom(y) < sdom(u)\) 的结论，\(y\) 不可能是 \(sdom(w)\) 的完全子孙节点。同时，\(y\) 也不会既是 \(idom(u)\) 的完全子孙节点又是 \(u\) 的祖先节点，因为如果存在这种情况，那么肯定存在一条从 \(r\) 到 \(sdom(y)\) 的树路径，后面跟着一条 \(sdom(y) = v_0, v_1, \ldots, v_k = y\) 的路径，其中对于 \(1 \leqslant i \leqslant k - 1\)，\(v_i > y\)，由于 \(y \geqslant idom(u)\)，所以 \(v_i > idom(u)\)，其后再跟一条从 \(y\) 到 \(u\) 的树路径，其中不包含 \(idom(u)\)，这样就组成了一条不包含 \(idom(u)\) 的从 \(r\) 到 \(u\) 的路径，而这与 idom 的定义矛盾。

  因为 \(idom(u) \xrightarrow{*} v \xrightarrow{+} u \xrightarrow{*} w\)，并且 \(idom(u) \xrightarrow{*} y \xrightarrow{*} w\)，又因为 \(y \xrightarrow{*} sdom(w) \xrightarrow{+} u\)，所以 \(y\) 只能放到位置 \(idom(u)\) 上，也就是 \(idom(u) = y\)。所以 \(idom(u)\) 位于路径 \(p\) 上，因为 \(p\) 是任意到 \(w\) 的路径，所以 \(idom(u)\) 是 \(w\) 的 dominator。 \(\Box\)

• COROLLARY 1. Let \(w \ne r\) and let \(u\) be a vertex for which \(sdom(u)\) is minimum among vertices \(u\) satisfying \(sdom(w) \xrightarrow{+} u \xrightarrow{*} w\). Then

  \[idom(w) = \begin{cases} sdom(w) &\text{if } sdom(w) = sdom(u), \\ idom(u) &\text{} otherwise. \end{cases}\]

  PROOF. 如果 \(sdom(u) = sdom(w)\)，则所有的其他可能的 u 取值肯定都满足根据 \(sdom(u) \geqslant sdom(w)\)。根据 THEOREM 2，\(idom(w) = sdom(w)\)。否则直接取 THEOREM 3 的结论。 \(\Box\)

• THEOREM 4. For any vertex \(w \ne r\), \(sdom(w) = min(\{v \mid (v, w) \in E\) and \(v < w\} \cup \{sdom(u) \mid u > w\) and there is an edge \((v, w)\) such that \(u \xrightarrow{*} v\})\).

  PROOF. 假设等式右边的表达式等于变量 \(x\)。我们首先证明 \(sdom(w) \leqslant x\)。假设 \((x, w) \in E\)，并且 \(x < w\)。那么，根据 \(sdom\) 的定义，\(sdom(w) \leqslant x\)。另外一方面，如果 \(x = sdom(u)\)，\(u > w\)，并且存在一条边 \((v, w)\)，\(u\) 到 \(v\) 存在树路径（\(u \xrightarrow{*} v\)）。根据 \(sdom\) 定义，存在一条路径 \(x = v_0, v_1, \ldots, v_j = u\)，其中对于 \(1 \leqslant i \leqslant j - 1\)，\(v_i > u > w\)。而树路径 \(u = v_j \rightarrow v_{j+1} \rightarrow \ldots \rightarrow v_{k-1} = v\) 中的节点 \(v_i\) 满足 \(v_i \geqslant u > w\)，对于 \(j \leqslant i \leqslant k - 1\)。从而也就有了路径 \(x = v_0, v_1, \ldots, v_{k-1} = v, v_k = w\)，其中对于 \(1 \leqslant i \leqslant k - 1\)，\(v_i > w\)，根据 \(sdom\) 定义，\(sdom(w) \leqslant x\)。

  然后需要再证明 \(sdom(w) \geqslant x\)。设 \(sdom(w) = v_0, v_1, \ldots, v_k = w\)，对于 \(1 \leqslant i \leqslant k - 1\)，\(v_i > w\)。当 \(k = 1\) 时，\((sdom(w), w) \in E\)，并且根据 Lemma 3，\(sdom(w) < w\)，因此 \(sdom(w) \geqslant x\)（\(x\) 是最小的此类 \(sdom(w)\)）。另一方面，当 \(k > 1\) 时，设 \(j\) 是满足条件 \(j \geqslant 1\) 并且 \(v_j \xrightarrow{*} v_{k-1}\) 的最小取值。 我们需要证明 \(v_i > v_j\)，其中 \(1 \leqslant i \leqslant j - 1\)。假设存在 \(v_i \leqslant v_j\)，\(1 \leqslant i \leqslant j - 1\)。根据 Lemma 1，从 \(v_i\) 到 \(v_j\) 存在一个公共祖先节点 \(v_{min}\)，从而满足 \(v_{min} \xrightarrow{*} v_j\)，这与 \(j\) 的定义矛盾。

  因为 \(sdom(w) = v_0\)，所以 \(sdom(w) \geqslant sdom(v_j)\)，又因为 \(x\) 是所有可能取值的最小值，所以 \(sdom(v_j) \geqslant x\)。\(sdom(w) \geqslant x\) 得证，所以 \(sdom(w) = x\)。 \(\Box\)

• 证明的逻辑关系

  Fig.3. 证明逻辑图

  graph LR; L1[LEMMA 1] --> L3[LEMMA 3]; L2[LEMMA 2] --> L4[LEMMA 4]; L3 --> L4; T1(THEOREM 1) --> L5[LEMMA 5]; L1 --> T2(THEOREM 2); L4 --> T2; L4 --> T3(THEOREM 3); L5 --> T3; T2 --> C1(COROLLARY 1); style C1 fill:#f9f,stroke:#333,stroke-width:4px; T3 --> C1; L1 --> T4(THEOREM 4); style T4 fill:#f9f,stroke:#333,stroke-width:4px; L3 --> T4;

算法及其高效实现

• 算法流程

  Step 1. Carry out a depth-first search of the problem graph. Number the vertices from 1 to \(n\) as they are reached during the search. Initialize the variables used in succeeding steps.

  Step 2. Compute the semidominators of all vertices by applying Theorem 4. Carry out the computation vertex by vertex in decreasing order by number.

  Step 3. Implicitly define the immediate dominator of each vertex by applying Corollary 1.

  Step 4. Explicitly define the immediate dominator of each vertex, carrying out the computation vertex by vertex in increasing order by number.

• 提前准备的数据结构

  Input

  \(succ(v)\): The set of vertices \(w\) such that \((v, w)\) is an edge of the graph.

  Computed

  \(parent(w)\): The vertex which is the parent of vertex \(w\) in the spanning tree generated by the search.

  \(pred(w)\): The set of vertices \(v\) such that \((v, w)\) is an edge of the graph.

  \(semi(w)\): A number defined as follows:

  • Before vertex \(w\) is numbered, \(semi(v) = 0\).

  • After \(w\) is numbered but before its semidominator is computed, \(semi(w)\) is the number of \(w\).

  • After the semidominator of \(w\) is computed, \(semi(w)\) is the number of the semidominator of \(w\).

  \(vertex(i)\): The vertex whose number is \(i\).

  \(bucket(w)\): A set of vertices whose semidominator is \(w\).

  \(dom(w)\): A vertex defined as follows:

  • After step 3, if the semidominator of \(w\) is its immediate dominator, then \(dom(w)\) is the immediate dominator of \(w\). Otherwise \(dom(w)\) is a vertex \(v\) whose number is smaller than \(w\) and whose immediate dominator is also \(w\)’s immediate dominator.

  • After step 4, \(dom(w)\) is the immediate dominator of \(w\).

• Step 1

  n := 0;
  for each v in V do pred(v) := NULL; semi(v) := 0 od;
  DFS(r);
  
  procedure DFS(vertex);
    begin
      semi(v) := n := n + 1;
      vertex(n) := v;
      comment initialize variables for steps 2, 3, and 4;
      for each w in succ(v) do
        if semi(w) = 0 then parent(w) := v; DFS(w) fi;
        add v to pred(w) od
    end DFS;
  

• Step 2 and 3

  comment initialize variables;
  for i := n by -1 until 2 do
    w := vertex(i);
  
    Step2:
    for each v in pred(w) do
      u := EVAL(v); if semi(u) < semi(w) then semi(w) := semi(u) fi od;
    add w to bucket(vertex(semi(w)));
    LINK(parent(w), w);
  
    step3:
    for each v in bucket(parent(w)) do
      delete v from bucket(parent(w));
      u := EVAL(v);
      dom(v) := if semi(u) < semi(v) then u
                else parent(w) fi
      od
    od;
  

  计算 \(sdom\) 和隐式计算 \(idom\) 是在一个节点的处理过程中一并进行的，而节点处理顺序根据逆先序进行。这里有两个操作，用于构建一个 \(forest\)，并从中提取信息，这个 \(forest\) 由图中的节点和满足 \(\{(parent(w), w) \mid w\) has been processed\(\}\) 的边构成：

  \(LINK(v, w)\): Add edge \((v, w)\) to the forest.

  \(EVAL(v)\): If \(v\) is the root of a tree in the forest, return \(v\). Otherwise, let \(r\) be the root of the tree in the forest which contains \(v\). Return any vertex \(u \ne r\) of minimum \(semi(u)\) on the path \(r \xrightarrow{*} v\).

  我们已经知道，通过Theorem 4可以求得某个节点的 semidominator，现在 \(semi(w) = min\{semi(EVAL(v)) \mid (v, w) \in E\}\)，\(semi(w)\) 就是 \(w\) 的 semidominator，理由如下：如果 \(v\) 小于 \(w\)，则 \(v\) 尚未被处理，\(v\) 还是 \(forest\) 中的一个顶点（没有被 \(LINK\)），并且 \(semi(v)\) 等于 \(v\) 的序号，所以 \(semi(EVAL(v))\) 等于 \(v\) 的序号，如果 \(v\) 大于 \(w\)，根据逆先序，\(v\) 要么是 \(w\) 的子节点，要么是 \(v\) 的兄弟节点，无论哪种情况，\(EVAL(v)\) 都会返回一个大于 \(w\)，并且是到 \(v\) 的树路径上的所有节点中 semidominator 最小的节点，\(semi(EVAL(v))\) 就是该 semidominator。因而 \(semi\) 的这个计算方式和Theorem 4完全吻合，可以用来计算 semidominator。

  上面算法中逆先序遍历节点，对于每个节点应用 \(semi(w) = min\{semi(EVAL(v)) \mid (v, w) \in E\}\)，由于是逆先序，所以序号大于 \(w\) 的节点都已经计算出了正确的 semidominator，所以计算结果一定是完备的。接着将 \(w\) 放入 \(bucket\) 中，建立和 semidominator 的关系，然后用 \(LINK\) 方法将 \(forest\) 向上扩展，代表 \(w\) 已经完成 semidominator 的计算。接着算法从 \(bucket(parent(w))\) 中取出节点 \(v\)，设 \(u = EVAL(v)\)，则 \(parent(w) \xrightarrow{+} u \xrightarrow{*} v\)，并且 \(u\) 是符合 \(sdom(u)\) 最小的节点。根据Corollary 1，当 \(semi(u) = semi(v)\) 时，\(idom(v) = sdom(v) = parent(w)\)，否则 \(idom(v) = idom(u)\)，算法里指示 \(dom(v) = u\) 来让Step 4中继续计算 \(dom(v)\)。

• Step 4

  for i := 2 until n do
    w := vertex(i);
    if dom(w) != vertex(semi(w)) then dom(w) := dom(dom(w)) fi;
    od
  dom(r) := 0;
  

  从小到大遍历是因为Step 3中 \(u < v\)。

• 例子

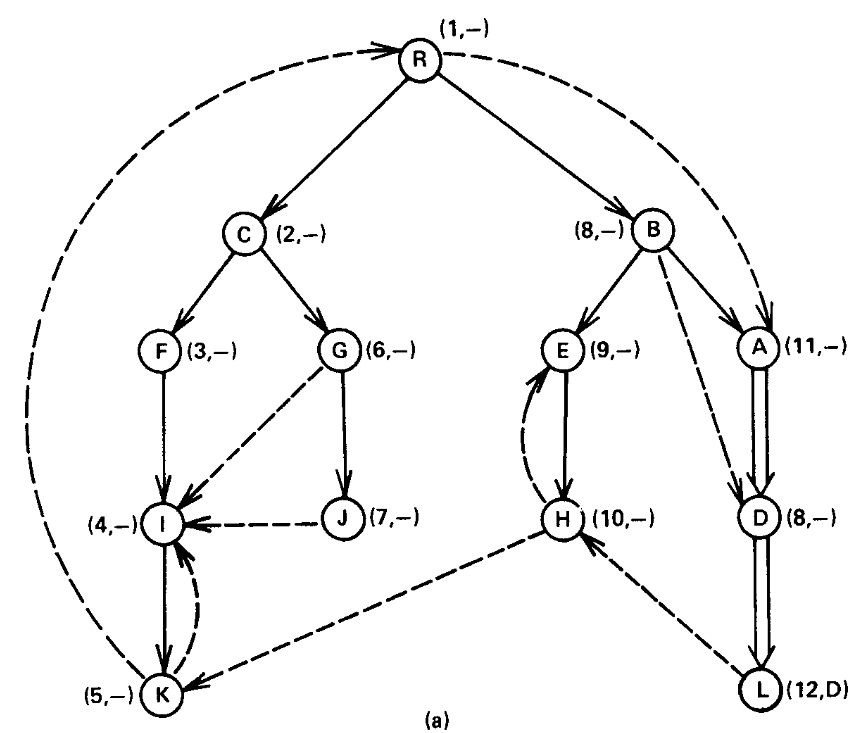
  Figure 4 is a snapshot of the graph just before vertex \(A\) is processed. Two edges \((B, A)\) and \((R, A)\) enter vertex \(A\), giving 8 (the number of \(B\)) and 1 (the number of \(R\)) as candidates for \(semi(A)\). The algorithm assigns \(semi(A) = 1\), places \(A\) in \(bucket(R)\), and adds edge \((B, A)\) to the \(forest\). Then the algorithm empties \(bucket(B)\), which contains only \(D\). \(EVAL(D)\) produces \(A\) as the vertex on the path \(B \xrightarrow{+} A \xrightarrow{*} D\) with minimum \(semi\). Since \(semi(A) = 1 < 8 = semi(D)\), \(idom(A) = idom(D)\) and the algorithm assigns \(dom(D) = A\).

  Fig. 4 Snapshot just before processing vertex \(A\). Double lines denote edges in \(forest\). Number in parentheses is \(semi\); letter in parentheses is \(dom\)

  

• LINK 和 EVAL 的实现

  简单的实现是用path compression来实现 \(EVAL\)。为了表示由 \(LINK\) 操作构造的 \(forest\)，需要引入两个数据结构 \(ancestor\) 和 \(label\)。\(ancestor(v)\) 表示 \(v\) 在 \(forest\) 中的父节点，初始为 0，代表无父节点，\(label(v)\) 表示节点 \(v\) 的 EVAL 值，初始为 \(v\) 本身。

  To carry out \(LINK(v, w)\), the algorithm assigns \(ancestor(w) := v\).

  procedure EVAL(v);
    if ancestor(v) = 0 then EVAL := v
      else COMPRESS(v); EVAL := label(v) fi;
  
  procedure COMPRESS(v);
    comment this procedure assumes ancestor(v) != 0;
    if ancestor(ancestor(v)) != 0 then
      COMPRESS(ancestor(v));
      if semi(label(ancestor(v))) < semi(label(v)) then
        label(v) := label(ancestor(v)) fi;
      ancestor(v) := ancestor(ancestor(v)) fi;
  

  复杂实现使用了path compression on balanced trees⁶ 的算法，让 \(LINK\) 操作构造了平衡树，\(EVAL\) 操作不变，从而让整个算法的执行速度有大幅提高。细节可以参考论文中的 1、2、5 小结。

  在讲这个算法前，首先介绍下EVAL-LINK-UPDATE问题。这个问题描述的是对于一个半群 \((S, \odot)\)，其中 \(\odot\) 代表一个符合结合律的任意操作，执行以下三类操作来构建和修改一个 \(forest\)，这个 \(forest\) 中的节点的 \(label\) 属于集合 \(S\)。

  \(EVAL(v)\): \(\odot(r, w) = label(r) \odot \ldots \odot label(w)\)

  \(LINK(v, w)\): \(parent(w) := v\)

  \(UPDATE(r, x)\): \(label(r) := x \odot label(r)\)

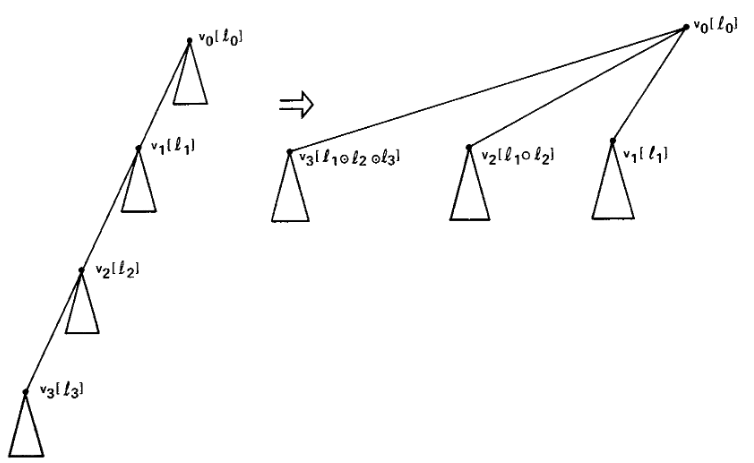
  现在的问题是如果按照定义的逻辑进行算法实现，性能会很慢，假设对于一个有 \(n\) 个节点 \(m\) 条边的图来说，\(LINK\) 构造了一个线性的树，则算法复杂度将会是 \(O(nm)\)。为了加快操作的执行效率，\(EVAL\) 操作可以利用path compression提高速度，如上面 \(EVAL\) 的简单实现所示（效果间 Fig 5）。

  Fig. 5 经过path compression后的图，三角形代表子树，中括号中代表 \(label\) 值。

  

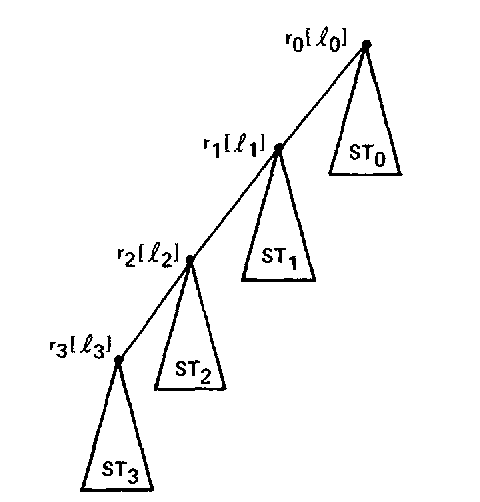
  有没有更加高效的算法呢？有的！如果 \(\odot\) 是一个比较操作，则可以通过构造一颗平衡的树来达到 EVAL 加速的目的。这棵树要满足以下条件，它由子树 \(ST_0, ST_1, \ldots, ST_k\) 构成，这些子树的根节点分别是 \(r_0, r_1, \ldots, r_k\)，这些节点在同一条路径 \(r_0 \rightarrow r_1 \rightarrow \ldots \rightarrow r_k\) 上，并且满足 \(label\) 递增或者递减关系，如下图所示：

  Fig. 6 \(label\) 满足 \(l_0 \preccurlyeq l_1 \preccurlyeq l_2 \preccurlyeq l_3\)

  

  改进的算法还需要引入另外两个数据结构 \(size\) 和 \(child\)，\(size(v)\) 表示当前子树 \(root\) 节点 \(v\) 的子孙节点个数，\(child(v)\) 表示 \(v\) 的某个是子树 \(root\) 的子节点。那么在 \(UPDATE\) 操作中，必须要保持子树 \(root\) 节点的 \(\odot\) 关系，所以做如下修改：

  procedure UPDATE(r, x),
    begin
      comment this procedure assumes size(O) = 0 and label(O) = infinite,
      label(r) = max (x, label(r)};
      if label(r) > label(child(r)) do
        rl := child(r),
        while label(r) > label(chlld(r1)) do
          if size(rl) + size(child(child(r1))) >= 2* stze(child(rl)) then
            parent(child(r1)) := rl, child(r1) = child(child(r1))
          else size(child(r1)) = size(r1);
            rl := parent(r1) = child(r1) fi od;
        label(r1) = label(r), child(r) = rl fi
      end UPDATE
  

  通过合并 \(root\) 节点小于 \(UPDATE\) 后的 \(v\) 的子树来保证子树 \(root\) 节点单调性。设 \(subsize\) 为一个子树的节点数，可以通过 \(subsize(r_l) = size(r_1) - size(child(r_1)) \geqslant size(chiid(r_l)) - size(child(child(r_1))) = subsize(child(r_l))\) 来判断子树合并的时候应该由谁做为父节点，以保证合并生成的新子树的相对平衡。

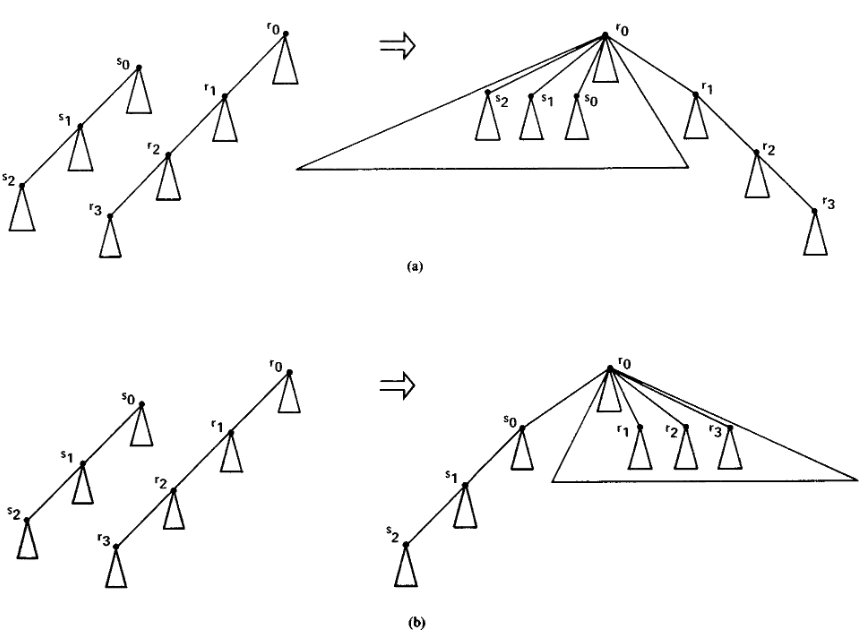
  接下来利用 \(UPDATE\) 操作来实现 \(LINK(v, w)\)。其中 \(v = r_0, r_1, \ldots, r_k，w = s_0, s_1, \ldots, s_l\)。首先先进行 \(UPDATE(w, label(v))\)，这样能确保 \(label(v) \preccurlyeq label(w)\)，然后判断 \(v\) 和 \(w\) 的 \(size\) 大小，合并 \(size\) 小的路径上的所有子树到 \(size\) 大的树的第一个子树中。由于 \(EVAL\) 操作不变，而作用域变成了子树范围，所以速度就能提高。效果见 Fig 7。

  procedure LINK(v, w),
    begin
      UPDATE(w, label(v)),
      size(v) := size(v) + size(w);
      s = w;
      if size(v) < 2 * size(w) then s <-> child(v) fi;
      while s != 0 do parent(s) = v; s = child(s) od
    end LINK;
  

  Fig. 7 (a) \(size(r_0) \geqslant size(s_0)\); (b) \(size(r_0) < size(s_0)\)

  

  把这个算法套用到求 \(sdom\) 的算法中，\(\odot(x) = min\{semi(label(x_i)) \mid r = x_0, x_1, \ldots, x_j = x, 0 \leqslant i \leqslant j\}\)，得到新的 \(LINK\) 操作如下：

  procedure LINK(v, w);
    begin
      comment this procedure assumes for convenience that size(O) = label(O) = semi(O) = 0;
      s: = w;
      while semi(label(w)) < semi(label(child(s))) do
        if size(s) + size(child(child(s))) >= 2 * size(child(s)) then
          parent(child(s)) := s; child(s) := child(child(s))
        else size(child(s)) := size(s);
          s := parent(s) := child(s) fi od;
      label(s) := label(w);
      size(v) := size(v) + size(w);
      if size(v) < 2 * size(w) then s, child(v) := child(v), s fi;
      while s != 0 do parent(s) := v; s := child(s) od
    end LINK;
  

  这里把 \(w\) 和 \(v\) 的 UPDATE 操作延后了一下。

• Hotspot(C.Click) 的实现

  和论文中的Algol伪代码几乎完全相同，甚至将结构体都以算法作者姓名命名，唯一的区别在于识别完idom后继续创建dominator tree，从而根据dominator tree算出每个节点的dominator depth。